快速排序

数据结构

快速排序（Quicksort) 在平均状况下，排序n个项目要O(nlogn)次比较。在最坏状况下则需要O(n2)次比较，但这种状况并不常见。它在排序效率同为O(nlogn)的几种排序方法中效率最高，因此经常被采用。

算法思想

设数组a中存放了n个数据元素，low为数组的低端下标，high为数组的高端下标，从数组a中任取一个元素（通常取a[low]）作为标准，调整数组a中各个元素的位置，使排在标准元素前面的元素的关键字均小于标准元素的关键字，排在标准元素后面的元素的关键字均大于或等于标准元素的关键字。（即标准元素被放在了未来排好序的数组中该标准元素应在的位置）然后，对这两个字数组中的元素分别再进行方法类同的递归快速排序。递归算法的结束条件是high <= low，即上界下表小于或等于下界下标。

对快速排序 （挖坑填数）进行形象化总结：

  1. i = L; j = R; 将基准数（pivot）挖出形成第一个坑a[i]。
  2. j– 由后向前找比它小的数，找到后挖出此数填入前一个坑a[i]中。
  3. i++ 由前向后找比它大的数，找到后也挖出此数填入前一个坑a[j]中。
  4. 再重复之行2，3二步，直到i == j，将基准数（pivot）填入a[i]中。
  5. 递归调用上述步骤，直到数组中全部元素从小到大排序完成。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void QuickSort(int a[], int low, int high)
/* 用递归方法对数据元素a[low]~a[high]进行快速排序 */
{
    int i = low, j = high;
    int temp = a[low];
    while (i < j)
    {
        while(i < j && temp <= a[j]) j--; //从数组右端扫描，找比基准小的数并赋给a[i]
        if (i < j)
        {
            a[i] = a[j];
            i++;
        }
       
        while (i < j && a[i] < temp) i++; //从数组左端扫描，找比基准大的数并赋给a[j]
        if (i < j)
        {
            a[j] = a[i];
            j--;
        }
    }
    a[i] = temp;
    /* 最后i == j */
    if (low < i) QuickSort(a, low, i - 1);
    if (i < high) QuickSort(a, j + 1, high);
}

排序算法性能比较

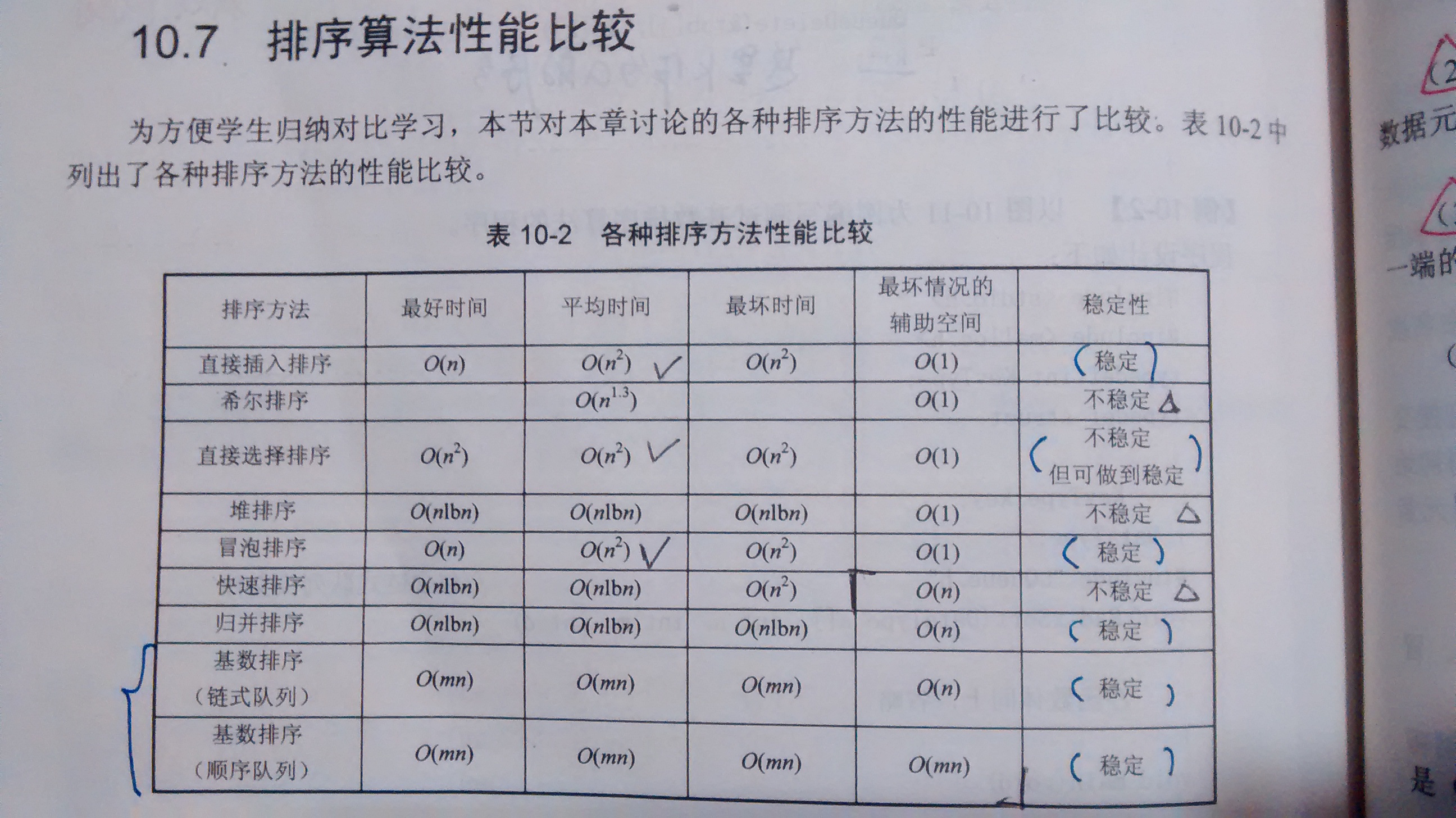
sort.jpg
文章目录
  1. 1. 算法思想
  2. 2. 排序算法性能比较
|